В файле (PDF) и в ссылках на сайты - статьи с описанием обобщенной динамики Ферхюльста - Рикера - Планка и ее связи с постоянной тонкой структуры
D.B. Volov. Specific behavior of one chaotic dynamics near the fine-structure constant http://arxiv.org/abs/1205.6091
http://chaosandcorrelation.org/Chaos/DV_1_5_2012.pdf
Volov_D__VTP_5_2011.pdf
http://www.sciteclibrary.ru/rus/catalog/pages/11612.html
Текст программы на MathCAD для воспроизведения бифуркационной диаграммы "четыре крыски" (Д.Б. Волов, Россия, Самара).

Диаграмма "четыре крыски".
Текст программы на MATLAB для воспроизведения бифуркационной диаграммы "четыре крыски". (А.П.Трунев, Торонто, Канада)
(улыбку надо заменить на двоеточие)
x(i+1)=-L(k)/(x(i)^2(exp(x(i))+alpha))
L=zeros(1,500);
y=zeros(1,128);
ly=zeros(1,128);
alpha=1/137.035999074;
dL=(3.7+exp(1.1989))/500;
for k=1:length(L)
for i=1:length(y)
if (k==1)
L(k)=-3.8;
y(k, =1;
=1;
ly(k, =log(y(k,
=log(y(k, );
);
else
if (i==1)
L(k)=L(k-1)+dL;
V=y(k-1,128)*y(k-1,128)*(exp(-y(k-1,128))+alpha);
y(k,i)=exp(L(k))/V;
ly(k,i)=log(y(k,i));
else
V1=y(k,i-1)*y(k,i-1)*(exp(-y(k,i-1))+alpha);
y(k,i)=exp(L(k))/V1;
ly(k,i)=log(y(k,i));
end
end
end
end
for i=1:128
plot(L,ly(:,i),'.k')
hold on
title('a=1/137');
xlabel('lnK');ylabel('lnx');
end
Результат:
http://chaosandcorrelation.org/AS/4rat.gif
Бифуркационная диаграмма "четыре крыски" одномерного отобрахения.
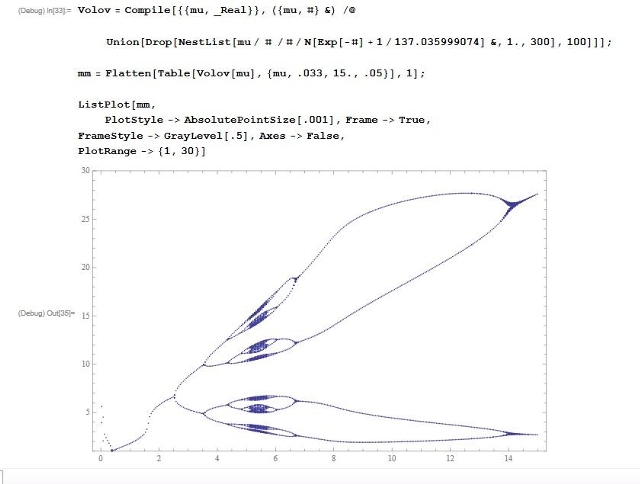
Код для Wolfram Mathematica 8 и результат (А.П.Трунев, Торонто, Канада):